在双碳目标的驱动下，航空领域越来越青睐于非传统的能源和推进系统，包括可再生航空燃料，燃氢发动机，电池或燃料电池驱动的电推进系统，分布式推进和多旋翼等。其中，电动多旋翼垂直起降( eVTOL) 飞行器由于飞行噪声低、环境友好、对地面基础设施依赖小等优势，在城市空中交通领域中的应用潜力巨大。然而，当前电池的能量密度过低，制约了 eVTOL 飞行器续航能力和载荷的提升。此外，相对于传统单旋翼直升机构型，更小直径的多旋翼要获得相同的推力，需以更高的转速旋转，故而使得旋翼效率更低。因此，在飞行器概念设计阶段，用简单且准确的分析方法来快速评估 eVTOL 飞行器的续航性能，有助于研究人员和企业理解航程、重量、速度和灵活性之间此消彼长的关系，对飞行器进行优化设计和任务规划，进而满足飞行时间和飞行半径等需求。

 

 

 

航程和航时是飞行器重要的性能参数，二者的评估需要考虑空气动力学特性、推进系统和飞行器的重量。传统飞机燃用液体化石燃料，应用 Breguet航程方程可为飞行器提供定性化的评估。新概念飞行器有很多新特点，如电驱动系统设计的一个重要因素是电池，常规电池动力运行过程中重量不变。Hepperle 等和 Patterson 等假设电池重量、放电速率和电压在放电过程中保持不变，推导了电池动力电推进飞行器的基本航程方程。实际上电池电容依赖于电池放电速率，即电容 － 放电速率效应。最广泛使用的考虑电容 － 放电速率效应的电池模型是Peukert 方程。

 

 

 

目前针对电动固定翼飞机的航程和航时估算，国内外学者开展了大量研究，考虑了真实电池放电过程的影响因素，较为准确地估算出电动飞机的航程和航时。Traub研究了考虑电池电容 － 放电速率效应的电池动力固定翼无人机最大平飞航程和航时时的最优电池重量系数，发现电池重量系数为飞机总重的 2 /3 时可获得最大航时，且与电池类型无关。对多旋翼飞行器续航性能的估计大多集中于悬停航时。Hnidka 等采用动量叶素( BEM) 理论来计算多旋翼飞行器悬停所需要的功率，并与完全测量的电池模型结合，来估计多旋翼飞行器悬停航时。Biczyski 等也提出了多旋翼飞行器悬停时间的估计方法，电池采用 Peukert 模型，气动阻力采用平方模型。Abdilla 等和 Gatti 等推导了考虑电池电容 － 放电速率效应的电池动力倾转机翼无人机的悬停航时。Gatti 等发现存在使得飞行器航时最大的最优的电池重量或电容。针对多旋翼飞行器前 飞 工 况，Godbole 等和 Cieslewski等将理想电池模型与阻力平方模型结合获得了多旋翼飞行器的航程和最优飞行速度。而同时考虑电池真实放电效应和气动阻力来估算多旋翼飞行器前飞工况续航性能的研究较少。Bauersfeld 等采用最新的 BEM 理论与机身阻力模型来计算多旋翼飞行器在给定速度下的气动阻力，电池动力学采用单一时间常数模型，首次提出了适用于多种多旋翼飞行 器 的 航 时、航程和最优飞行速度评估方法。Hwang 等采用动量理论来计算多旋翼无人机前飞所需要的功率，并与 Peukert 电池模型结合来计算飞行器的航时和最优飞行速度。但在电动旋翼飞行器续航性能理论分析中，电池容量是一个重要影响因素。当前尚无电动多旋翼飞行器最优电池容量分析方法，因此亟需建立相应的方法，以便在概念设计阶段进行初步优化设计。

 

 

鉴于此，本文尝试结合动量理论和 Peukert 电池放电模型，建立了电动多旋翼垂直起降飞行器最优续航性能理论分析方法，并基于某型六旋翼电动垂直起降飞行器平台，对其最优续航性能进行了分析。分析结果对未来电动多旋翼飞行器设计具有一定的参考意义。

 

分析方法

 

1  功率需求模型

 

 

 

2  电池放电模型

 

 

 

3续航性能计算方法

 

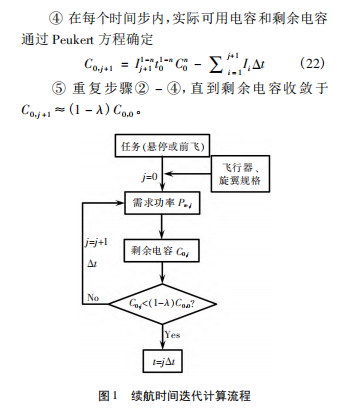
实际上，悬停和水平匀速前飞的续航时间均可通过上述方法计算得到。水平匀速前飞工况由于机身气动阻力与飞行速度之间存在非线性关系，因而存在久航速度和远航速度; 在一定电池电容下，通过改变飞行速度值，对飞行速度进行寻优，可获得久航速度和远航速度; 进而通过改变电池电容值，在久航速度和远航速度下对电池电容进行寻优，可获得最优的久航和远航电池重量。

 

4

 

模型参数

 

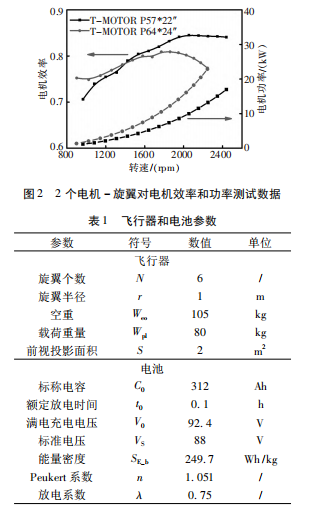
本文分析基于六旋翼电动垂直起降飞行器平台，电池选用锂电池，飞行器和电池主要参数如表 1所示。典型旋翼效率在 0.5 ～ 0.7之间，本文取值 0.6。电机效率根据电机制造商提供的 2 个电机－旋翼对 30 组拉力测试台测试数据进行估计，如图2 所示。可以看出，电机效率在 0.7 ～ 0.85之间，而在较大转速进和功率范围内，电机效率在 0.8 ～0.85之间。因此，本文选取一个固定的电机效率为0.8。在前飞工况，阻力系数强烈依赖于机身形状。本文飞行器平台尺寸、外形以及速度与汽车类似，因此本文阻力系数取为汽车行驶时的值 0.96。文中对单一变量进行优化时，假设其他设计参数为固定值，分析结果在飞行器概念设计阶段仍具有一定的指导意义。进一步的方案设计则需要采用多参数多目标优化设计方法。

 

 

 

结果与分析

 

1  悬停最优续航时间

 

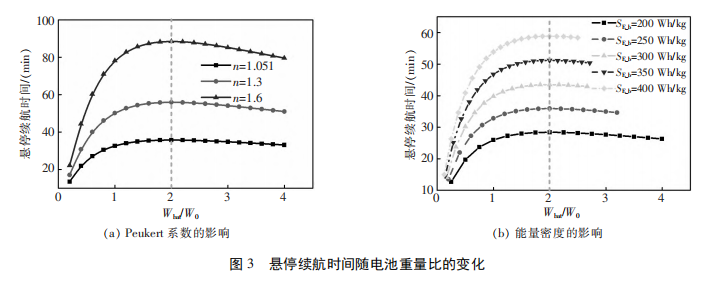
飞行器续航时间取决于电池电容。由式(13)可知，电池标称电容与电池重量成正比。同时，式(19) 表明电池重量为机身和载荷重量的两倍时，续航时间最大。因此，研究续航时间与电池 － 空重重量比( Wbat /W0 ) 的关系，可更直观地分析出满足最优续航时间所需的条件。图 3 给出了在不同电池 Peu-kert 系数和能量密度的情况下，悬停续航时间随电池重量比的变化。可以看出，虽然在 Wbat /W0 = 2时，悬停续航时间最大，且与电池 Peukert 系数和能量密度无关; 但在 Wbat /W0 ＜ 1 时，悬停续航时间对Wbat /W0 的变化最为敏感; 当 Wbat /W0 ＞ 1 之后，悬停续航时间变化较为平缓，继续增大电池重量对提升悬停续航时间效果不明显。因此，对于设计人员来说，虽然存在最优电池重量比，但为了获得飞行器重量和悬停续航时间之间的平衡，电池重量应不超过飞行器空重。此外还可以看出，提高电池 Peukert 系数和能量密度有助于提高悬停续航时间。

 

 

 

2  水平匀速前飞最优续航时间和里程

 

在一定电池电容下，存在最久和最远续航飞行速度。图 4 给出了不同电池重量比、Peukert 系数和能量密度对最优飞行速度的影响。可以看出，由于电池电容增加，电池重量增大，因而飞行器重量也增大，久航和远航飞行速度均随电池重量比增大而增大。Peukert 系数和能量密度对久航飞行速度无影响，能量密度对远航飞行速度也无影响，但 Peukert系数 n 增大会降低远航飞行速度。

 

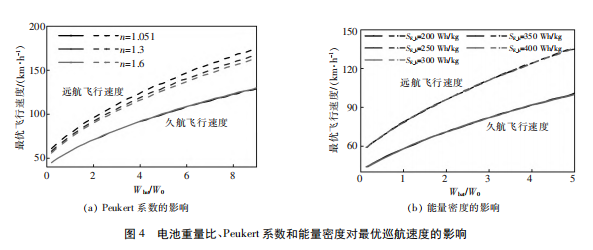
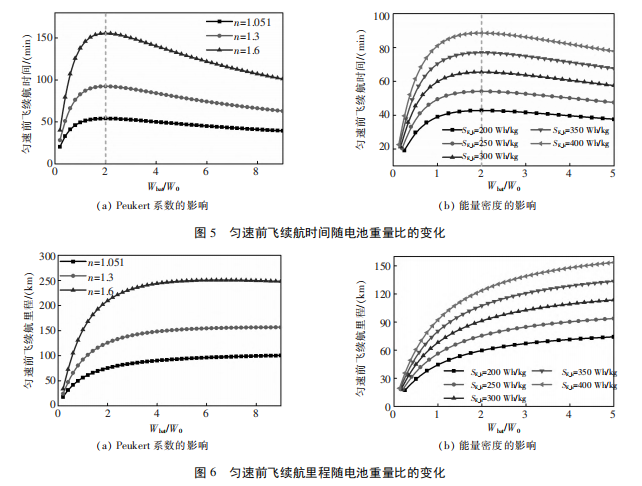
图 5 给出了在不同电池 Peukert 系数和能量密度的情况下，久航飞行速度下匀速前飞续航时间随电池重量比的变化。可以看出，与悬停续航时间类似，当 Wbat /W0 近似为 2 时，续航时间最大，且与电池 Peukert 系数和能量密度无关。这与电池动力固定翼飞行器巡航飞行时具有相似之处。同样，在Wbat /W0 ＜ 1 时，匀速前飞续航时间对 Wbat /W0 的变化最为敏感; 在 Wbat /W0 ＞ 1 之后，继续增加电池重量对提升续航时间效果不显著。因此，为了获得飞行器重量和前飞续航时间之间的平衡，电池重量应不超过飞行器空重。此外，提高电池 Peukert 系数和能量密度也有助于提高巡航续航时间。

 

 

 

在不同电池 Peukert 系数和能量密度的情况下，最优续航里程飞行速度下匀速前飞续航里程随电池重量比的变化关系如图 6 所示。可以看出，对于续航里程，在 n 较大( n = 1． 6) 时存在最优电池重量比Wbat /W0≈6． 6，此时电池重量于飞行器总重量的占比达 87% 。在 n 靠近 1 时，续航里程随电池重量比的增大逐渐增大。不同电池 Peukert 系数和能量密度情况下，当 Wbat /W0 ＜ 2 时，续航里程对 Wbat /W0 的变化最为敏感; 在 Wbat /W0 ＞ 2 之后，继续增加电池重量对于提升续航里程效果已不显著。为了获得飞行器重量和前飞续航里程之间的平衡，电池重量应不超过飞行器空重的两倍。此外，提高电池 Peukert系数和能量密度也有助于提高前飞续航里程。

 

结论

 

本文结合动量理论和 Peukert 电池放电模型，建立了电动多旋翼垂直起降飞行器最优续航性能理论分析方法，并基于六旋翼电动垂直起降飞行器平台进行了最优续航性能分析，主要结论如下:

 

 

 

悬停和匀速前 飞 均 存 在 最 优 的 电 池 重 量 比Wbat /W0 = 2 使得续航时间最大，且该比值与电池参数无 关; 对 于 续 航 里 程，最优电池重量比与电池Peukert 系数 n 有关。这与固定翼飞机的最优续航性能特征相似。

 

 

 

当电池重量比 Wbat /W0 ＜ 1 时，悬停和匀速前飞续航时间对 Wbat /W0 的变化最为敏感; 对于续航里程，当 Wbat /W0 ＜ 2 时，续航里程变化最为敏感。在此比值之后继续增加电池重量，对于提升续航性能效果已不显著。

 

 

 

为了获得飞行器重量和续航性能之间的最佳平衡，电池重量比需低于最优电池重量比，并需采用多参数多目标优化设计方法进行进一步优化设计。